Flowing

Note:

In practice, users may sometimes prefer to suppress flow arrows graphically, since it can result in a simpler diagram; however, this is a decision to be made by software like PISE, which displays Proofscape diagrams. At the level of the Meson script, flow arrows are always created and added to the logical graph, according to the rules described in this section.

While deduction arrows indicate the logical structure of a proof, it can be useful to have another type of arrow, to help direct the reader to examine the nodes of the proof in a certain order.

For example, it is good to guide the reader to the introduction of new symbols, before visiting nodes that use those symbols.

For this, Proofscape diagrams offer flow arrows, which are drawn dashed instead of solid.

Example:

A, therefore B. C implies D.

Try it

There are three keywords in the flow keyword category:

Table 8 flow keywords

now

next

claim

and the rule governing the drawing of flow arrows is as follows:

A flow arrow will be drawn from node A to node B when all the keywords between A and B (if any) are in the modal and/or flow categories. In particular, a flow arrow will be drawn if there are no keywords at all between A and B.

Thus,

A, therefore B. Let I. Then C, using D.

Try it

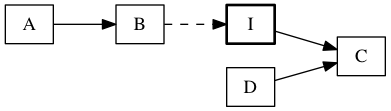
Suppose S. Then A. Now let I. Then B, by A and C.

Try it

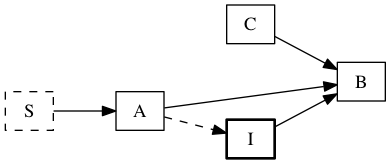
Notice that in this last case there are two arrows leaving node A, and the purpose of the flow arrow is to tell us that we should consider the intr node I first, before considering node B.