Part 7: Navigation Groups#
In Part 2: Annotations and Part 3: Sphinx Pages, we saw a few minimal examples of chart widgets (review Listing 2, Listing 7, and Listing 8), and in Part 4: Doc Widgets we started to see some doc widgets (review Listing 11). Both of these fall under the general heading of Nav Widgets, which are widgets whose job is to navigate content in other panels.
When you get into the practice of navigating content in other panels, the question soon arises: which other panels? In the examples we explored earlier in this tutorial, generally what happened was that you clicked on a widget, say a chart widget, which caused a new chart panel to open, and then clicking on other chart widgets continued to navigate that same panel.
In many cases this basic behavior is just what’s desired, but eventually cases will arise in which you want something different. Namely, you might want either of the following behaviors:
Have two widgets in a single notes page, which navigate two different chart panels, or two different doc panels.
Have widgets on two different notes pages, both of which control one and the same chart panel, or one and the same doc panel.
In this part of the tutorial you’ll learn to achieve both of these behaviors, using Navigation groups.
Setup#
Before we actually look at navigation groups, we’ll pause to set up a few things. None of this setup is necessary to use navigation groups themselves. Everything we do here merely serves to give us a plausible example to look at, and to motivate a look at the important topic of dependency declarations in particular.
Declaring dependencies#
In the examples we’re going to build next, we will, for the first time in this tutorial, want to refer to objects defined in another Proofscape repo, outside of our own. Namely, we’ll be using the Toeplitz Project Literature Library.
In order to do this, we have to tell the system the version number at which we’re taking this external repo. We do this by defining a dependencies object in The root module. See Dependency declarations.
Find our repo’s root module in the “File System” tab of the sidebar
(the __.pfsc file in the root directory), and double-click to open.
As yet, the file is empty. Add the following code to it now:
1deps = {
2 "gh.toepproj.lit": "v0.23.1",
3}
By doing this, we’ve declared that we’re taking the gh.toepproj.lit repo at version
0.23.1. We won’t build just yet though, since we haven’t yet actually imported anything
from this repo, or defined anything new of our own.
A new section in our Sphinx pages#
In Part 3: Sphinx Pages, we started a collection of Sphinx pages, in which we imagined we were recording notes from our math courses. Let’s extend that now, by adding a new section for a new (imaginary) course.
Using the same technique as last time (you can review it here), add the following new submodules now, in the order shown:
Under… |
…make new submodule… |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
When you’re done, you should have the files and directories depicted here:
Next we need to get the new files started, and update one old toctree directive
as well. Make sure your files are as in the listings below.
=================
Math Course Notes
=================
In these pages, I'm going to record notes on proofs
from my math courses.
.. toctree::
:maxdepth: 2
AbstAlgFall2023/index
AlgNoThSpring2025/index
====================================
Algebraic Number Theory, Spring 2025
====================================
In addition to the course textbook, we're going to have some extra enrichment,
by looking at some of the historical texts and papers in which the subject
originated.
.. toctree::
:maxdepth: 2
Origins/index
=======
Origins
=======
We're looking at Hilbert's *Zahlbericht*.
I'll organize my notes by class day.
.. toctree::
wk7mo
wk7we
==============
Week 7, Monday
==============
UNDER CONSTRUCTION...
=================
Week 7, Wednesday
=================
UNDER CONSTRUCTION...
The last two files are deliberately left incomplete. We’ll fill them in later.
Build clean#
Finally, it’s time to build. Since we modified the toctree of a Sphinx page we
built before (see Listing 27), this time we want to ask
the system to do a clean build. This will rebuild all pages, in particular updating
their tables of contents to link to our new pages.
Right-click the repo root directory in the “File System” view, and click “Build Clean.”
Note
The first time you try to build our example repo since declaring our new dependency
on gh.toepproj.lit, PISE may notify you that this dependency has not
been built yet at the required version, and ask if you want to build it now. Say yes,
and it will build automatically. You’ll only have to do this once. (If by chance
you happen to have already built gh.toepproj.lit@v0.23.1 before, then you won’t
see this prompt at all.)
After the build completes, you should be able to find your new Sphinx pages over in the “Structure” view.
One page navigating two panels#
Now that our preliminary setup is out of the way, we’re ready to take our first look at navigation groups.
Without groups#
For sake of contrast, we’ll start by building a page that does not make use of
navigation groups. Open the wk7mo.rst file, replace its contents with those in
Listing 32, and build.
1==============
2Week 7, Monday
3==============
4
5.. pfsc::
6
7 from gh.toepproj.lit.H.ilbert.ZB import Thm119, Thm117
8
9We looked at Hilbert's Thm 119, which shows how primes different from $\ell$ factor
10in the $\ell$th cyclotomic field.
11
12I want to talk about :pfsc-chart:`this step <Thm119.Pf.S130.A2>`.
13Here $\mathfrak{p}$ is a prime ideal coprime to $\ell$.
14The proof cites a step from the proof of Thm 117, where we factored $\ell$.
15I want to go back and look at how we got that factorization, so let's
16:pfsc-chart:`open the proof of Thm 117 <Thm117.Pf.A5>`.
17
18The form of the factorization is easier to remember, if you remember how we
19get it. It comes from
20:pfsc-chart:`factoring the minimal polynomial <Thm117.Pf.A4>` that defines
21the field, and then just plugging in $x = 1$.
After the build completes, double-click the wk7mo Sphinx page in the “Structure” tab
to open it.
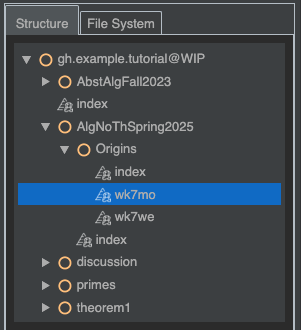
Your page should load, showing some text with three chart widgets.
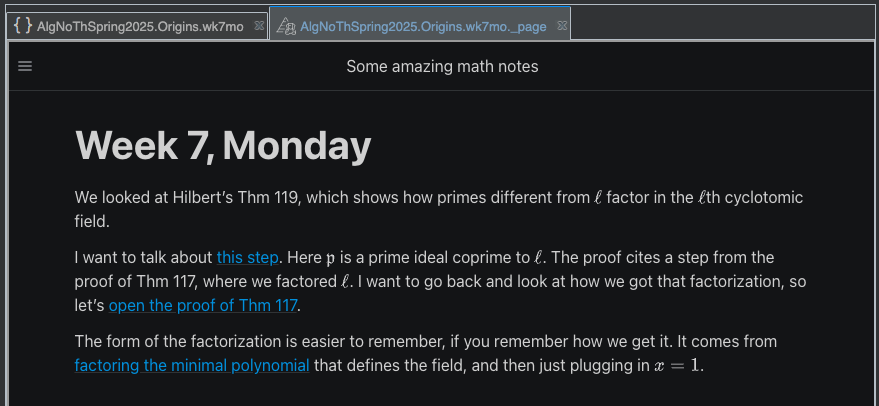
Read through the page, clicking the chart widgets as you go, and watch the chart panel that loads and navigates beside the page.
When you clicked the second chart widget, the one that says, “open the proof of Thm 117,” you probably noticed that Thm 117 and its proof were added to the same chart panel that was first opened to show Thm 119. This is one way of using chart panels in PISE. You can load many different deductions at once, in a single panel. In cases like the present one, where one proof cites a node from another, you can even see the citation drawn out as a deduction edge going from one proof to the other.
However, there are other ways to use chart panels. When you show multiple deductions in a single panel, as we’re currently doing, then looking back and forth at different deductions means panning back and forth. This can be fine, especially if you use the overview inset to help you pan, and keep track of what’s on the board. In the present case, you can also go back and click the various widgets again, to automatically pan back and forth.
Another option would be to load Thm 117 and its proof in a second chart panel. Then, looking back and forth at theorems 117 and 119 would mean switching between different tabs in PISE. This isn’t necessarily better or worse, just another way of doing things.
With groups#
Let’s suppose we want to try using two panels, one for each theorem. We can achieve that by (finally!) using navigation groups.
Go back to your editor panel, and we’ll now rework the widgets somewhat. As you can see in Listing 33, we will now use the Substitution format for the second and third widgets, which allows us to keep them inline in the paragraphs where they belong, while defining as many of their fields as we wish.
In particular, in the new block definitions for these widgets, we’re now
using the group field, to assign them to their own navigation group.
1==============
2Week 7, Monday
3==============
4
5.. pfsc::
6
7 from gh.toepproj.lit.H.ilbert.ZB import Thm119, Thm117
8
9We looked at Hilbert's Thm 119, which shows how primes different from $\ell$ factor
10in the $\ell$th cyclotomic field.
11
12I want to talk about :pfsc-chart:`this step <Thm119.Pf.S130.A2>`.
13Here $\mathfrak{p}$ is a prime ideal coprime to $\ell$.
14The proof cites a step from the proof of Thm 117, where we factored $\ell$.
15I want to go back and look at how we got that factorization, so let's
16|open the proof of Thm 117|.
17
18.. |open the proof of Thm 117| pfsc-chart::
19 :view: Thm117.Pf.A5
20 :group: "Thm117"
21
22The form of the factorization is easier to remember, if you remember how we
23get it. It comes from |factoring the minimal polynomial|
24that defines the field, and then just plugging in $x = 1$.
25
26.. |factoring the minimal polynomial| pfsc-chart::
27 :view: Thm117.Pf.A4
28 :group: "Thm117"
Tip
The value of the group field is a string or integer of your choice. If you’re writing a long
page, it’s a good idea to use a meaningful name, like the "Thm117" we’ve used here, to
help you remember the purpose of each group. But on a short page, like ours, we could have
also just used the integer 2, say, for the second group.
After updating your file to match Listing 33, build again, and close the existing chart panel. Your Sphinx page shouldn’t look any different, but as you once again read through and click the widgets, you should find new behavior: The first widget opens a chart panel to show Thm 119 as before, but the second one now opens a second chart panel, to show Thm 117.
If you go back now and repeatedly click the different widgets in this page, the appropriate chart panels will automatically be selected and made visible.
Question: The second and third widgets now belong to a group named "Thm117", but to
what group does the first widget belong?
Answer: When you don’t define a widget’s group, then it belongs to what is called The default group.
Two pages navigating one panel#
Above, we learned how to make two widgets within a single page navigate two different panels. Now we’re going to learn how to do the opposite: make widgets belonging to different pages navigate a single panel.
Without groups#
As in the previous part, we’re going to start by seeing what happens when we work without navigation groups.
Open the wk7we.rst source file, replace its contents with those in
Listing 34, and build.
1=================
2Week 7, Wednesday
3=================
4
5.. pfsc::
6
7 from gh.toepproj.lit.H.ilbert.ZB import Thm119
8
9Carrying on with Thm 119, we were looking at
10:pfsc-chart:`this step <Thm119.Pf.S130.A2>`. I want to now talk about the role
11this step is playing in this proof.
12
13We want to show that :pfsc-chart:`$f' = f$ <Thm119.Pf.A160>`, and we're working
14toward one half of that, namely that :pfsc-chart:`$f' \\geq f$ <Thm119.Pf.A150>`.
15What we know about $f$ is :pfsc-chart:`this <Thm119.Thm.I2>`. So it would
16suffice to show that we've got :pfsc-chart:`the same congruence <Thm119.Pf.A140>`
17(essentially), with $f'$ in place of $f$.
18
19And we're going to get this from :pfsc-chart:`here <Thm119.Pf.A120>`.
20We know that $\zeta^\ell = 1$, and that the value of $\zeta^g$ for any integer
21$g$ depends only on the residue of $g$ mod $\ell$.
22Therefore :pfsc-chart:`the subproof we've been looking at <Thm119.Pf.S130>`
23supplies the critical observation we need.
Open the built Sphinx page, and take a look.
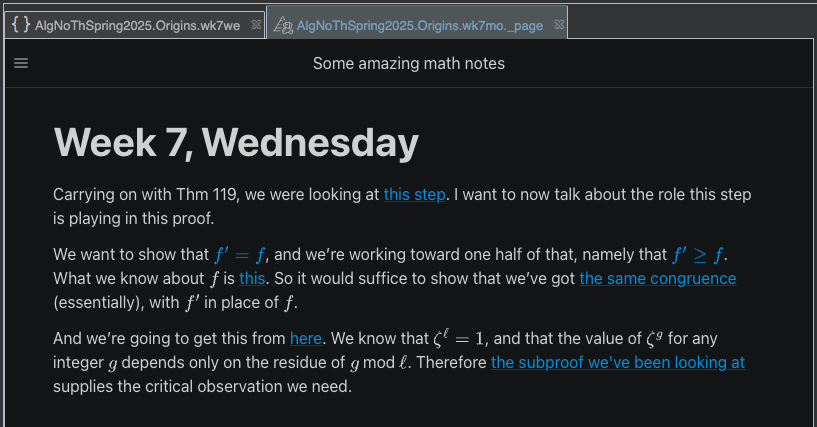
Don’t click any of the widgets yet. (If you did, just close the chart panel.)
Our purpose now is to think about how this page, the “Wednesday page” from our imaginary course notes, is going to work in combination with our previous page, our “Monday page.” Specifically, we want to see what happens if you click the widgets in “Monday,” and then move on and click the widgets in “Wednesday.” How do they work together?
Therefore, find the “Previous” link now, at the bottom left corner of the current page,
and click this to navigate back to “Monday.” Then click through all the widgets on that page, to open the associated chart panels. Then click the “Next” page link at the bottom right,
to get back to “Wednesday.”
Now, finally, click the first widget on the “Wednesday” page. What happens? We get a brand new chart panel to navigate.
Is this what we wanted? Maybe. But maybe not. Maybe we wanted our Wednesday notes to integrate more smoothly with the Monday discussion, by continuing to navigate one of the same chart panels that was already open. Naturally, we’ll achieve this next by using navigation groups.
With groups#
In order to make our two pages share a common chart panel, we’re going to have to revise both.
In Listing 35, we switch the first widget in our “Monday” page into the Substitution format,
and set .. for its group field:
1==============
2Week 7, Monday
3==============
4
5.. pfsc::
6
7 from gh.toepproj.lit.H.ilbert.ZB import Thm119, Thm117
8
9We looked at Hilbert's Thm 119, which shows how primes different from $\ell$ factor
10in the $\ell$th cyclotomic field.
11
12I want to talk about |this step|.
13Here $\mathfrak{p}$ is a prime ideal coprime to $\ell$.
14The proof cites a step from the proof of Thm 117, where we factored $\ell$.
15I want to go back and look at how we got that factorization, so let's
16|open the proof of Thm 117|.
17
18.. |this step| pfsc-chart::
19 :view: Thm119.Pf.S130.A2
20 :group: ".."
21
22.. |open the proof of Thm 117| pfsc-chart::
23 :view: Thm117.Pf.A5
24 :group: "Thm117"
25
26The form of the factorization is easier to remember, if you remember how we
27get it. It comes from |factoring the minimal polynomial|
28that defines the field, and then just plugging in $x = 1$.
29
30.. |factoring the minimal polynomial| pfsc-chart::
31 :view: Thm117.Pf.A4
32 :group: "Thm117"
In Listing 36, we use a ctl widget to set ..
as the default value of the group field for all chart widgets in our “Wednesday” page.
(We could have used a ctl widget in Listing 35 as well, but we’ve done it
this way to demonstrate two different methods.)
1=================
2Week 7, Wednesday
3=================
4
5.. pfsc::
6
7 from gh.toepproj.lit.H.ilbert.ZB import Thm119
8
9.. pfsc-ctl::
10 :default_chart_group: ".."
11
12Carrying on with Thm 119, we were looking at
13:pfsc-chart:`this step <Thm119.Pf.S130.A2>`. I want to now talk about the role
14this step is playing in this proof.
15
16We want to show that :pfsc-chart:`$f' = f$ <Thm119.Pf.A160>`, and we're working
17toward one half of that, namely that :pfsc-chart:`$f' \\geq f$ <Thm119.Pf.A150>`.
18What we know about $f$ is :pfsc-chart:`this <Thm119.Thm.I2>`. So it would
19suffice to show that we've got :pfsc-chart:`the same congruence <Thm119.Pf.A140>`
20(essentially), with $f'$ in place of $f$.
21
22And we're going to get this from :pfsc-chart:`here <Thm119.Pf.A120>`.
23We know that $\zeta^\ell = 1$, and that the value of $\zeta^g$ for any integer
24$g$ depends only on the residue of $g$ mod $\ell$.
25Therefore :pfsc-chart:`the subproof we've been looking at <Thm119.Pf.S130>`
26supplies the critical observation we need.
As explained under NAMESPACE in the reference docs, by setting .. as
the group of some of our chart widgets, we have put them all into a single group
that can be joined by any widgets defined under the
gh.example.tutorial/AlgNoThSpring2025/Origins directory of our Proofscape repo.
Thus, as long as we’re recording log pages under this directory, we can use this shared
group to make our widgets share navigation panels.
After updating both pages to the versions above, go ahead and rebuild. When the build completes, we want to examine the whole experience from the start one more time, so we must once more:
Close all existing chart panels
Navigate back to “Monday”
Click all widgets
Navigate back to “Wednesday”
And then finally, click the first widget on the “Wednesday” page.
This time, as we continue our discussion of Thm 119 and its proof, the widgets on
our new page continue using an existing panel that was opened when we clicked
through our “Monday” discussion.
This is what we wanted, and we achieved it by setting group equal to .., so
that widgets on different pages could join a common group. Again, see
Navigation groups in the reference section for further explanation.
Summary#
You have learned how to use navigation groups to:
Make two widgets on the same page navigate two different panels
Make widgets on different pages navigate a single, common panel
Along the way, you also learned how to:
Declare dependencies on external Proofscape repos