WOLOG

It is common in English-language proofs to find the phrase, “without loss of generality,” sometimes abbreviated as “w.o.l.o.g.” or “WOLOG”.

When we write WOLOG in a proof, what we mean is that it is a proof by cases, but we need only examine one case, because there is an easy way to reduce all other cases to this one.

Note that this is not the same thing as a proof by cases in which one case is examined, while the others are dismissed as being “similar” (and perhaps left as exercises). That is just an abridged proof by cases. The distinguishing characteristic of WOLOG is the reduction or transformation of the other cases to the examined one.

Sometimes the method of reduction is indicated or hinted, while other times it is considered too obvious to be worth mentioning. Accordingly, there are two ways to encode WOLOG in Proofscape: one for when the reduction method is given, and one for when it is not.

WOLOG without reduction method

When no demonstration is given as to the method of reducing the other cases to the one examined, simply flow to a supp node, and add the wolog modifier after the name of the node:

supp S10 wolog {
        # ...
}

For example,

Listing 61 A proof using wolog without a method

deduc Thm {
    supp S {
        sy="$S$"
    }
    asrt A {
        sy="$A$"
    }
    meson="Suppose S. Then A."
}


deduc Pf of Thm.A {

    asrt B {
        sy="$B$"
    }

    supp T wolog {
        sy="$T$"
    }

    asrt C {
        sy="$C$"
    }

    meson="
    From Thm.S get B.
    Now suppose T. Then C, by B, hence Thm.A.
    "
}

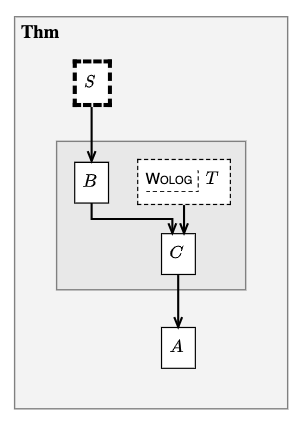
Fig. 22 A proof using wolog without a method

WOLOG with reduction method

When the proof does include some demonstration of how the remaining cases are to be reduced to the examined one, this typically means that, like in most demonstrations, some deduction arcs must be involved. But we cannot deduce a supp node, so we need another way to represent this in Proofscape.

For this purpose, mthd nodes are allowed to take the wolog modifier:

mthd M20 wolog {
    # ...
}

The phrase on the mthd node’s label will often begin with a present participle, such as “replacing…” or even just “assuming…”. The latter form can serve as a catch-all if nothing else works.

Example:

Listing 62 A proof using wolog with a method

deduc Thm {
    supp S {
        sy="$S$"
    }
    asrt A {
        sy="$A$"
    }
    meson="Suppose S. Then A."
}

deduc Pf of Thm.A {

    asrt B {
        sy="$B$"
    }

    mthd M wolog {
        en="
        Adding an
        appropriate constant
        to $f(x)$
        "
    }

    asrt C {
        sy="$C$"
    }

    meson="
    From Thm.S get B.
    Then C, applying M, hence Thm.A.
    "
}

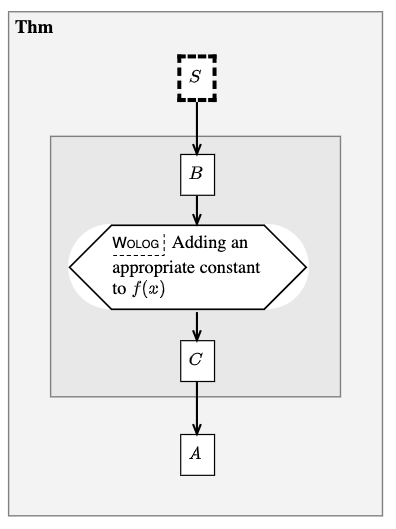
Fig. 23 A proof using wolog with a method