Node Types

The basic node types of Proofscape serve various purposes like making assertions, introducing defined symbols, making assumptions, etc. Examples can be seen in Fig. 10, and the code that generates these nodes in Listing 56.

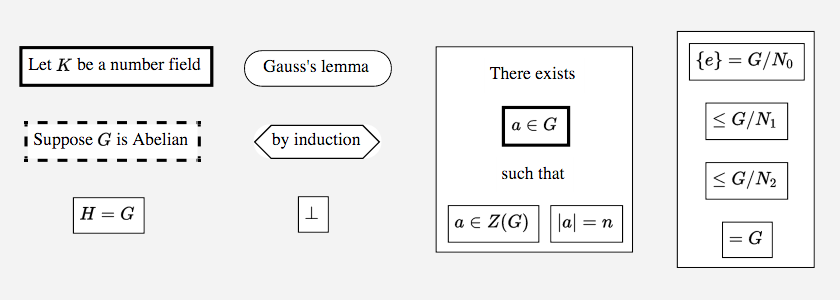
Fig. 10 Examples of all basic node types

Listing 56 Code to generate the basic node examples

intr I10 {
    en="Let $K$ be a number field"
}
supp S20 {
    en="Suppose $G$ is Abelian"
}
asrt A30 {
    sy="$H = G$"
}
cite C40 {
    en="Gauss's lemma"
}
mthd M50 {
    en="by induction"
}
flse F60 {}

exis E70 {
    en="There exists % such that"
    intr I {
        sy="$a \in G$"
    }
    asrt A1 {
        sy="$a \in Z(G)$"
    }
    asrt A2 {
        sy="$|a| = n$"
    }
}

rels R80 {
    asrt A1 {
        sy="$\{e\} = G/N_0$"
    }
    asrt A2 {
        sy="$\leq G/N_1$"
    }
    asrt A3 {
        sy="$\leq G/N_2$"
    }
    asrt A4 {
        sy="$= G$"
    }
}

Assertion nodes

The asrt or “assertion” node type is for stating assertions. Because the arrows in a Proofscape diagram indicate the logic of the proof, inferential language like “therefore” etc. should be omitted from the labels of asrt nodes.

The label on an asrt node should contain only an assertion itself, not any inferential language like “therefore” etc.

For example, a proof in the group theory literature might conclude with a statement like, “Therefore \(H = G\).” When encoded in Proofscape, we would use an asrt node with a label of “\(H = G\),” omitting “Therefore.”

Example:

asrt A30 {
    sy="$H = G$"
}

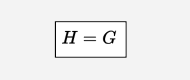
Fig. 11 An asrt or “assertion” node

Node naming tips:

Legal node names use alphanumerics and underscores, and begin with letters.

A good convention, demonstrated in Listing 56, is to use an initial letter corresponding to the node type, followed by a sequence number. When transcribing a proof from the literature, it is a good idea to increment the sequence number by tens, so that missed nodes can easily be inserted later. And start with ten, not zero.

Intro nodes

Introducing symbols to stand for various objects is a part of all mathematical proofs. In Proofscape this is done on intr a.k.a. “introduction” or “intro” nodes.

Whereas asrt nodes are rectangular with ordinary boundary (Fig. 11), intr nodes are rectangular with bold boundary (Fig. 12). This is a metaphor for the introduction of objects and symbols by fiat.

Example:

intr I10 {
    en="Let $K$ be a number field"
}

Fig. 12 An intr or “intro” node

It is common practice in mathematical works for some definitions to persist for a whole section, a whole chapter, or even for an entire work. For this Proofscape provides a feature called Running Definitions. Therefore:

Use intr nodes for the introduction of objects and symbols local to a proof, but consider using Running Definitions for definitions that persist over several proofs in a work.

Intro nodes are one of two node types that are called modal nodes, the other being supposition nodes, which we cover next. This distinction becomes relevant when writing Meson scripts, as covered under Modals.

Supposition nodes

“Supposition” nodes have type supp and are for stating the premises of a theorem, as well as for introducing new assumptions during the course of a proof. See Contradictions and Cases.

Example:

supp S20 {
    en="Suppose $G$ is Abelian"
}

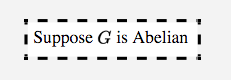
Fig. 13 A supp or “supposition” node

Supp nodes are rectangular with dashed boundary, a metaphor for their hypothetical nature.

Along with intro nodes, supp nodes are modal nodes. See Modals.

Existential nodes

The existential or exis node type handles formulas like,

There exists \(a \in G\) such that \(a \in Z(G)\) and \(|a| = n\).

in which an object is both stated to exist, and simultaneously introduced for further use:

exis E70 {
    en="There exists % such that"
    intr I {
        sy="$a \in G$"
    }
    asrt A1 {
        sy="$a \in Z(G)$"
    }
    asrt A2 {
        sy="$|a| = n$"
    }
}

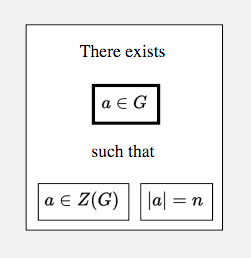
Fig. 14 An exis or “existential” node

Since the exis node itself makes an assertion, its boundary is rectangular and in plain style like an ordinary assertion node. Meanwhile it features internal intro and assertion nodes for the components of the statement.

Tip:

Within a compound node there is little motivation to employ the “number by tens” node naming convention, since you are unlikely to accidentally omit part of the statement.

As such this is the first compound node type that we have considered, i.e. a node type containing nested node definitions within its own definition.

In Fig. 14 there is one internal intr node, introducing the object which is stated to exist, and two internal asrt nodes, stating properties of that object.

The internal nodes can then be used individually in the Meson script, and are referenced via relative libpaths such as E70.I, E70.A1, and E70.A2 in this example. (The entire node can be used as a whole in a Meson script as well.)

Note that the label text for the exis node itself specifies the connective text, “There exists … such that” and a % character is used to separate the two parts of this text.

exis nodes:

• The label for the exis node defines the connective text, for example, “There exists … such that”, and uses a % character to separate the two parts.

• Define internal intr and asrt nodes for the components of the statement.

• In your Meson script, refer to the internal nodes using relative libpaths like E.I or E.A1.

Method nodes

Sometimes proofs indicate how an inference follows by explicitly naming or describing the method that is involved. For example this can involve phrases like:

• “by induction”

• “repeating this process”

• “substituting \(c\) for \(x\)”

In Proofscape such indications belong on mthd or “method” nodes.

Example:

mthd M50 {
    en="by induction"
}

Fig. 15 A mthd or “method” node

In order to understand how method nodes are linked into Meson scripts, see Methods.

Citation nodes

In Proofscape you should use internal citations whenever possible. This means that if a proof cites a lemma, and that lemma is available in some Proofscape content repo, the lemma should be imported (see Imports) and referenced directly in the proof’s Meson script. Similarly, if the proof cites a step from another proof, or any other node that has already been made available in a Proofscape content repo, it should be imported and used directly.

For cases where you need to cite something that is not (yet) available, you can make an external citation, using the cite or “citation” node type.

Example:

cite C40 {
    en="Gauss's lemma"
}

Fig. 16 An external citation using a cite or “citation” node

When possible, import and use existing nodes when one deduction refers to other deductions in whole or in part. These are called internal citations. For cases where this is not possible, make external citations using the cite node type.

Citation nodes will often play a temporary role (like the Special Nodes), serving as a placeholder until certain content can be made available.

Falsum nodes

Proof by contradiction or reductio ad absurdum is a staple of mathematical proof. The point at which a contradiction is reached is marked in Proofscape by a falsum or flse node.

Graphically, a falsum node looks like an assertion node (plain, solid boundary) whose label simply displays the “uptack” or “falsum” symbol often used to indicate absurdity or contradiction in formal logical systems.

Since the label for a flse node is predefined, there is no need to define anything inside the node definition braces.

Example:

flse F60 {}

Fig. 17 A flse or “falsum” node

Use a flse node to terminate a proof by contradiction. Do not define a label, since the label is automatic.

See Contradictions and Cases for examples of how the flse node is linked into the proof.

Relation chain nodes

In derivations it is common to make sequential assertions of the form

\[E_1 \:\: R_1 \:\: E_2\]

\[E_2 \:\: R_2 \:\: E_3\]

\[\ldots\]

\[E_n \:\: R_n \:\: E_{n+1}\]

in which the \(E_i\) are expressions and the \(R_i\) binary relations such as \(=\), \(\lt\), \(\gt\), etc. In such cases it is standard practice to concatenate these relations, as

\[E_1 \:\: R_1 \:\: E_2\]

\[\:\:\:\:\:\: R_2 \:\: E_3\]

\[\ldots\]

\[\:\:\:\:\:\:\:\:\:\: R_n \:\: E_{n+1}\]

so that intermediate expressions are not repeated. In proofs we often find that such a “relation chain” may be used as a whole in support of some claim, or that individual relations within the chain may need to be cited one at a time, or proved one at a time.

In order to support these patterns, Proofscape provides the rels or “relation chain” node type.

Example:

rels R80 {
    asrt A1 {
        sy="$\{e\} = G/N_0$"
    }
    asrt A2 {
        sy="$\leq G/N_1$"
    }
    asrt A3 {
        sy="$\leq G/N_2$"
    }
    asrt A4 {
        sy="$= G$"
    }
}

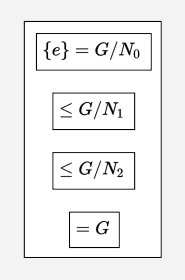
Fig. 18 A rels or “relation chain” node

Each relation is given on an asrt node defined within the rels node. In the initial relation we write both the left-hand and right-hand expressions, whereas for subsequent relations we omit the left-hand side.

Much as we saw earlier for Existential nodes, it is then possible to refer to the rels node itself – R80 in this example – as well as to refer to its subnodes using relative libpaths such as R80.A1, or R80.A2.

Use rels nodes so that the relations forming a “relation chain” can be cited both en bloc and individually.