Contradictions and Cases

Proof by contradiction and proof by cases are two common forms for mathematical proofs. Recalling the general node format (Listing 52), both of these proof structures are encoded using node MODIFIERS.

Proof by contradiction

Proofs by contradiction use the contra modifier.

To encode a proof by contradiction:

• Deduce a flse node from a set of nodes (often just two) that are mutually contradictory.

• Link the flse node to a supp node using the contra modifier.

Example:

Listing 59 A proof by contradiction

deduc Thm {
    supp S {
        sy="$S$"
    }
    asrt A {
        sy="$A$"
    }
    meson="Suppose S. Then A."
}

deduc Pf of Thm.A {

    supp T {
        en="Suppose not $A$."
    }

    asrt B {
        sy="$B$"
    }

    asrt C {
        sy="$C$"
    }

    asrt D {
        sy="$D$"
    }

    flse F contra T {}

    meson = "
    Suppose T. Then B and C. From C get D, using Thm.S, hence F, by B.
    Therefore Thm.A.
    "
}

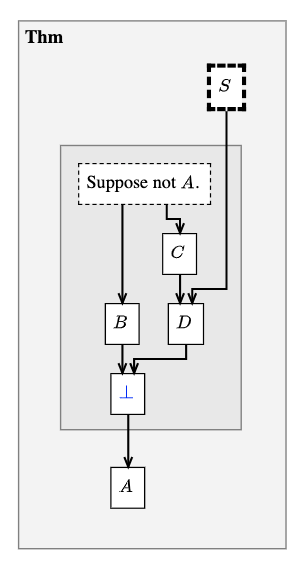
Fig. 20 A proof by contradiction

When a proof is displayed in PISE, the contra modifier activates the “up tack” or falsum symbol on the flse node, so that hovering highlights the contradicted supp node, and clicking brings it on screen.

Proof by cases

Proofs by cases use the versus modifier.

To encode a proof by cases:

• Use a set of subdeduc nodes, one for each case.

• Start each subdeduc with a supp node, indicating the assumption that defines the case.

• On one of these supp nodes, use the versus modifier to link it with the alternative cases.

• Deduce the common conclusion, citing each of the subdeduc nodes as reason.

Example:

Listing 60 A proof by cases

deduc Thm {
    supp S {
        sy="$S$"
    }
    asrt A {
        sy="$A$"
    }
    meson="Suppose S. Then A."
}

deduc Pf of Thm.A {

    subdeduc caseX {
        supp X {
            sy="$X$"
        }
        asrt B {
            sy="$B$"
        }
        asrt A {
            sy="$A$"
        }
        meson = "Suppose X. Then B, hence A, by Thm.S."
    }

    subdeduc caseY {
        supp Y versus caseX.X {
            sy="$Y$"
        }
        asrt C {
            sy="$C$"
        }
        asrt A {
            sy="$A$"
        }
        meson = "Suppose Y. Then C by Thm.S, hence A."
    }

    meson = "Thm.A by caseX and caseY."

}

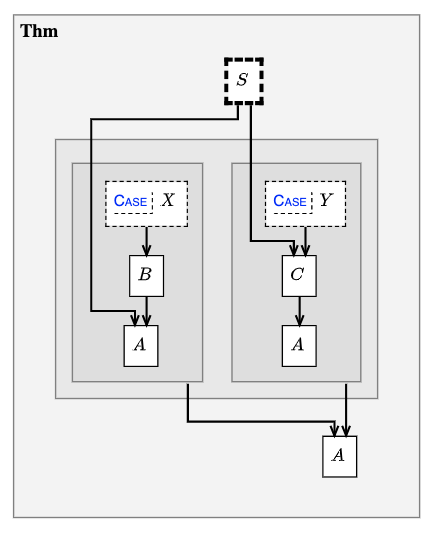
Fig. 21 A proof by cases

When a proof is displayed in PISE, the versus modifier adds a “CASE” label to each of the supp nodes that define the cases. The “CASE” label is activated, so that hovering highlights the case supp nodes, and clicking brings them on screen.

Using auxiliary deducs

It is often a good idea to write skeletal proofs in each subdeduc node, while writing a separate deduc to fill in the argument, so that the subdeduc can be expanded and collapsed.

An example of this technique can be seen in a proof by cases, each part of which is a proof by contradiction, in the proof of FLT for regular primes, from Hilbert’s Zahlbericht.