Combining inference and support#

Now that we have both the inf and sup keyword categories, we have to understand how they work together.

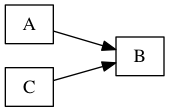
As a first example, try putting so and by together:

A, so B, by C.
../../_images/AsoBbyC.png

Try it

Pop Quiz#

What graph do you suppose is produced by the following Meson script?

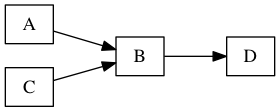
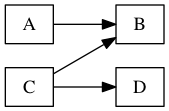
A so B by C therefore D

It’s clear that there will be three arrows:

  • so draws an arrow from A to B

  • by draws an arrow from C to B

  • therefore draws an arrow that terminates at D

But where will the arrow terminating at D begin? From B or from C? In other words, what are we saying D follows from?

Try it

Answer:

RIGHT

WRONG

quiz_right

quiz_wrong

The Meson script is saying that D follows from B, not from C.

Conceptually, we might say that Meson is somewhat biased toward a “forward flow” of deduction, in the sense that “by” or support statements should be thought of as nested parenthetically within an overall “so” or inference flow.

Thus, A so B gets us an arrow from A to B, then the by C parenthetically nudges in an arrow from C to B, and then we resume the overall forward flow with an arrow from B to D. To be precise:

An inf keyword always draws a deduction arrow from the most recently inferred node (like B in this example), NOT from any nodes that may have been mentioned in support (like C in this example).

Recap#

Using just the language features we have considered so far, we can already build up a fairly complex graph:

A, so B, therefore C by D and E. Hence F, using G, so H.
../../_images/Fancy1.png

Try it

Remember, the punctuation and word variation are just there to make the script more pleasant for a human being, and the very same graph could have been produced by a simpler but more monotonous sounding script:

A so B so C by D and E so F by G so H

This is noted in order to demonstrate how simple the Meson language actually is, but please, don’t write scripts like this!